Root Finding
The goal of this exercise is to learn how to numerically solve nonlinear algebraic equations. The general form of such equations is often written as:
which implies that our goal is to find a value for x such that the function f(x)
is 0. That is, we seek the roots of this function. The key to root-finding is to first
plot the function. Because we are considering nonlinear equations we can encounter
functions that have no real roots (consider 
), a finite number of roots (consider 
), or an infinite number of roots (consider 
). So without first understanding our function, generally by plotting
it in real space, we are doomed to failure.
Root-Finding is generally an iterative process. That is, we make a guess for our root and then successively improve our guess until we converge to a satisfactory solution. We will begin by discussing bracketing, a topic closely related to Root-Finding. Then we will consider three iterative methods:
Bracketing
A root of the function f(x) is bracketed if we have determined two values of the independent variable x such that the root lies between them. Generally the function values at the bracket edges will be of opposite value, so we can check for the existence of a bracket by checking whether the product of the two function values. That is, if x=a and x=b form a bracket, then f(a)*f(b)<0. This is not always true, though, because there are some special cases in which this is not true. A typical bracket (shaded) is depicted in the figure below.
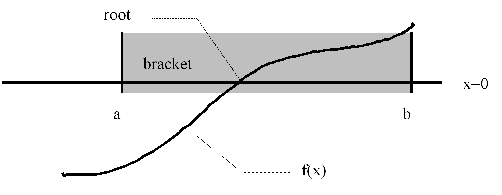
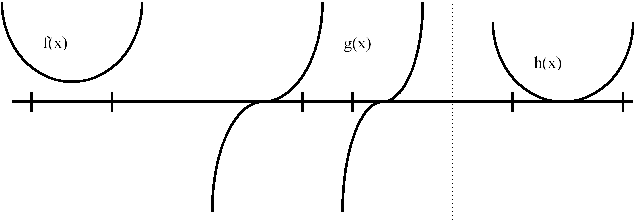
This is a relatively simple picture of a bracket. Some of the more complex situations that may arise are shown in the next figure. In the leftmost part of this figure [f(x)], there are no roots so we must be careful in trying to blindly bracket roots. This is a good reason to plot functions before trying to find roots. In the middle function in this figure [g(x)], the small vertical lines would seem to form a bracket, as their function values are of opposite sign. This is not the case, though because there is no root between these points. The difficulty here is that there is a singularity between these points. In the rightmost function [h(x)], there is a root between the two vertical lines but they do not seem to form a root because their function evaluations are not of opposite sign. This problem has arisen because the root is a double root. That is, the function just touches the line x=o. The bottom line, here, is that you must plot your function before you attempt to find a root.
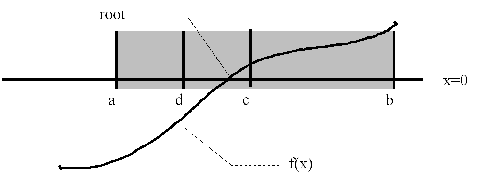
Once we have bracketed a root, we must locate the exact location of that root to some desired accuracy. Bisection is a relatively slow, but extremely reliable technique for solving algebraic equations in one variable (root-finding). The algorithm is based on the assumption that you can first bracket the root. Once a root is bracketed, you converge to a root by continually cutting the interval in half, always retaining the interval that contains the root. This procedure continues until convergence is achieved. This process is demonstrated in the figure below. The bracket on the interval [a,b] is halved by the line at x=c. Since the root now lies on the interval [a,c], we now use the bracket on this new interval. Halving the interval [a,c] by inserting a line at the point x=d creates two new potential brackets. The root lies on [d,c], so that now forms our new bracket. It should now be apparent how this process will lead to continuously smaller brackets, and the process can be continued until we've reached some desired accuracy defined by the width of the most current bracket.
This technique is most easily explained by example. Here we will consider a case where we seek the roots of f(x)=x*sin(x)-1. The first step in successive approximations is to solve explicitly for x in terms of a more complex function of x. That is if we seek values of x that yield f(x)=0, then we first solve for x, giving x=g(x), where g(x) depends on the particular problem. An obvious choice for our model problem is
,
while a less obvious choice would be
.
These can then be iterated to convergence. The process is to make a guess for the root (based on a plot of the function), insert that guess into the right hand side of the equations above, and then obtain a new guess for the root. This is then repeated until the results don't change from iteration to iteration. One question is, which of the two (or more) choices do we use for the iteration? The pragmatic answer is to try whichever is easier to implement and switch to the other if there is a problem. Note that this will not always be successful! You just have to try it out.
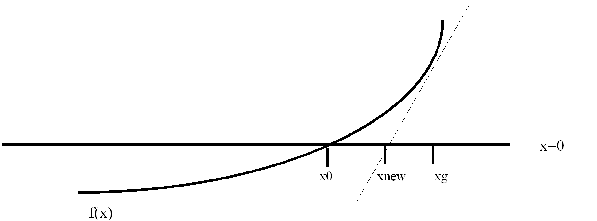
Newton's method is a faster, but less reliable, technique for root-finding. It is used quite often for practical applications. The method begins by expanding the function of interest in a Taylor's series about some point which we think might be the root. If we call this guess for the root xg then we can expand f(x) as
Here f'(xg) represents the first derivative of the function at the point xg. Also, we have truncated the series to two terms. If we now evaluate this series at the actual root, which we'll call x0, then we obtain:
Because x0 is a root (by definition), then f(x0)=0 and we can thus solve for x0. This gives
We can now use this to converge to a root. We start with a guess for a root and then evaluate the function above, providing an estimate for the root. We take this new estimate, plug it into the equation, and further update the root. This process proceeds until we converge. A graphical representation of this process is shown in the figure below. Here we start with the guess, and then extrapolate the tangent to the function down to the x-axis. The crossing point of this tangent becomes our new guess for the root (xnew). This is then repeated to convergence. The Taylor's series derivation above is equivalent to this process of drawing successive tangents to the curve.
